El Número de Oro – (PHI) La
Proporción Divina
Y la Sucesión de Fibonacci
El número de oro,
número dorado, sección áurea, razón áurea, razón dorada, media áurea,
proporción áurea y divina proporción, representado por la letra griega F
(fi) o Phi (en honor al escultor griego Fidias), es el número irracional:
Observa el orden de los números: 0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,…….Conocida como la serie de Fibonacci en honor al matemático italiano que la desarrolló.
Se comienza en 0 y el siguiente número es 1. De ahí en
adelante cada término siguiente se produce mediante la suma de los dos números
anteriores. Se empieza la serie sumando 0 más 1, que es igual a 1, luego 1
más1, que es igual a 2, sigue 1 más 2, que es igual a 3, 2 más 3, que es igual
a 5, luego 3 más 5, que es igual a 8 y se sigue la secuencia, 8 + 5 = 13, 13 +
8 = 21, 21 + 13 = 34, la suma puede seguirse indefinidamente. Lo peculiar de esta serie es que si
dividimos el número siguiente entre el número anterior, el resultado se va
aproximando al valor del número de oro según los números se van haciendo
mayores.
Se trata de un número que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción. Esta proporción se encuentra tanto en algunas figuras geométricas como en las partes de un cuerpo, y en la naturaleza como relación entre cuerpos, en la morfología de diversos elementos tales como caracolas, nervaduras de las hojas de algunos árboles, el grosor de las ramas, proporciones humanas, etc.

Historia del Número de Oro
El número áureo o la proporción áurea se estudió desde la antigüedad, ya que aparece regularmente en geometría. Se conoce ya de su existencia en los pentágonos regulares y pentáculos (pentagrama –estrella) de las tabletas sumerias de alrededor del 3200 a. C.
En la antigua Grecia se utilizó para establecer las proporciones de los templos, tanto en su planta como en sus fachadas. Por aquel entonces no recibía ningún nombre especial, ya que era algo tan familiar entre los antiguos griegos que "la división de un segmento en media extrema y razón" era conocido generalmente como "la sección". En el Partenón, Fidias también lo aplicó en la composición de las esculturas. (la denominación Fi, por ser la primera letra de su nombre, la efectuó en 1900 el matemático Mark Barr en su honor).

El Partenón, mostrando los rectángulos áureos usados posiblemente en su
construcción.
Platón (circa 428-347 a. C.), consideró la sección áurea como la mejor de todas las relaciones matemáticas y la llave a la física del cosmos. La sección áurea se usó mucho en el Renacimiento, particularmente en las artes plásticas y la arquitectura. Se consideraba la proporción perfecta entre los lados de un rectángulo. Da Vinci hizo las ilustraciones para una disertación publicada por Luca Pacioli en 1509 titulada De Divina Proportione, quizás la referencia más temprana en la literatura a otro de sus nombres, el de "Divina Proporción". Este libro contiene los dibujos hechos por Leonardo da Vinci de los cinco sólidos platónicos. Es probable que fuera Leonardo quien diera por primera vez el nombre de sección áurea. En 1525, Alberto Durero publica ´´Instrucción sobre la medida con regla y compás de figuras planas y sólidas donde describe cómo trazar con regla y compás la espiral basada en la sección áurea, que se conoce como “espiral de Durero”.
Platón (circa 428-347 a. C.), consideró la sección áurea como la mejor de todas las relaciones matemáticas y la llave a la física del cosmos. La sección áurea se usó mucho en el Renacimiento, particularmente en las artes plásticas y la arquitectura. Se consideraba la proporción perfecta entre los lados de un rectángulo. Da Vinci hizo las ilustraciones para una disertación publicada por Luca Pacioli en 1509 titulada De Divina Proportione, quizás la referencia más temprana en la literatura a otro de sus nombres, el de "Divina Proporción". Este libro contiene los dibujos hechos por Leonardo da Vinci de los cinco sólidos platónicos. Es probable que fuera Leonardo quien diera por primera vez el nombre de sección áurea. En 1525, Alberto Durero publica ´´Instrucción sobre la medida con regla y compás de figuras planas y sólidas donde describe cómo trazar con regla y compás la espiral basada en la sección áurea, que se conoce como “espiral de Durero”.
El rostro de la Gioconda proporcionado con rectángulos
áureos.
Los artistas del renacimiento utilizaron la sección áurea en múltiples ocasiones tanto en pintura, escultura como arquitectura para lograr el equilibrio y la belleza. Leonardo da Vinci, por ejemplo, la utilizó para definir todas las proporciones fundamentales en su pintura La última cena, desde las dimensiones de la mesa, hasta la disposición de Cristo y los discípulos sentados, así como las proporciones de las paredes y ventanas al fondo.
Leonardo da Vinci, en su cuadro de la Gioconda (o Mona Lisa) utilizó rectángulos áureos para plasmar el rostro de Mona Lisa. Se pueden localizar muchos detalles de su rostro, empezando porque el mismo rostro se encuadra en un rectángulo áureo.
El astrónomo Johannes Kepler (1571-1630), descubridor de la naturaleza elíptica de las órbitas de los planetas alrededor del Sol, mencionó también la divina proporción: “La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional. El primero lo podemos comparar a una medida de oro; el segundo lo debemos denominar una joya preciosa”. Y, creyente como era dijo: "no cabe duda de que Dios es un gran matemático"
Hoy en día la sección áurea se puede ver en multitud de diseños. El más conocido y difundido sería la medida de las tarjetas de crédito, la cual también sigue dicho patrón, así como nuestro carné de identidad y también en las cajetillas de cigarrillos. En la arquitectura moderna sigue usándose; por ejemplo, está presente en el conocido edificio de la ONU en Nueva York, el cual no es más que un gran prisma rectangular cuya cara mayor sigue las citadas proporciones.
La sección áurea en la naturaleza
En la naturaleza, hay muchos elementos relacionados con la sección áurea:
Según el propio Leonardo de Pisa Fibonacci, en su Libro de los ábacos, la secuencia puede ayudar a calcular casi perfectamente el número de pares de conejos n meses después de que una primera pareja comienza a reproducirse (suponiendo que los conejos se empiezan a reproducir cuando tienen dos meses de edad).
La relación entre la cantidad de abejas macho y abejas hembra en un panal.
La relación entre la distancia entre las espiras del interior espiralado de cualquier caracol (no sólo del nautilus)
La relación entre los lados de un pentáculo. (Pentagrama)
La relación entre los lados de un pentágono.
La disposición de los pétalos de las flores (elnúmero áureo en la botánica recibe el nombre de Ley de Ludwig).
La distribución de las hojas en un tallo
La relación entre las nervaduras de las hojas de los árboles
La relación entre el grosor de las ramas principales y el tronco, o entre las ramas principales y las secundarias (el grosor de una y equivale a F tomando como unidad la rama superior).
La distancia entre las espirales de una piña.
La Anatomía de los humanos se basa en una relación Phi exacta, así vemos que:
La relación entre la altura de un ser humano y la altura de su ombligo.
La relación entre la distancia del hombro a los dedos y la distancia del codo a los dedos.
La relación entre la altura de la cadera y la altura de la rodilla.
La relación entre el primer hueso de los dedos (metacarpiano) y la primera falange, o entre la primera y la segunda, o entre la segunda y la tercera, si dividimos todo es phi.
La relación entre el diametro de la boca y el de la nariz
Es phi la relación entre el diámetro externo de los ojos y la línea inter-pupilar
Cuando la tráquea se divide en sus bronquios, si se mide el diámetro de los bronquios por el de la tráquea se obtiene phi, o el de la aorta con sus dos ramas terminales (ilíacas primitivas).
Está comprobado que la mayor cantidad de números phi en el cuerpo y el rostro hacen que la mayoría de las personas reconozcan a esos individuos como lindos, bellos y proporcionados. Si se miden los números phi de una población determinada y se la compara con una población de modelos publicitarios, estos últimos resultan acercarse más al número phi. La sección áurea en el arte:
Relaciones arquitectónicas en las Pirámides de Egipto.
La relación entre las partes, el techo y las columnas del Partenón, en Atenas (s. V a. C.).
En los violines, la ubicación de las efes (los “oídos”, u orificios en la tapa) se relaciona con el número áureo.
El número áureo aparece en las relaciones entre altura y ancho de los objetos y personas que aparecen en las obras de Miguel Ángel, Durero y Da Vinci, entre otros.
Las relaciones entre articulaciones en el hombre de Vitruvio y en otras obras de Leonardo da Vinci.
En las estructuras formales de las sonatas de Mozart, en la Quinta Sinfonía de Beethoven, en obras de Schubert y Debussý (estos compositores probablemente compusieron estas relaciones de manera inconsciente, basándose en equilibrios de masas sonoras).
En la pág. 61 de la novela de Dan Brown El código Da Vinci aparece una versión desordenada de los primeros ocho números de Fibonacci (13, 3, 2, 21, 1, 1, 8, 5), que funcionan como una pista dejada por el curador del museo del Louvre, Jacques Saunière. En las pp. 121 a 123 explica algunas de las apariciones de este número fi (1,618) en la naturaleza.
En el episodio “Sabotaje” de la serie de televisión NUMB3RS (primera temporada, 2005), el genio de la matemática Charlie Eppes menciona que el número fi se encuentra en la estructura de los cristales, en la espiral de las galaxias y en la concha del nautilus.
Arte Póvera, movimiento artístico italiano de los años 1960, muchas de cuyas obras se basan en esta sucesión.
En la cinta de Darren Aronofsky Pi, el orden del caos el personaje central, Max Cohen, explica la relación que hay entre los números de Fibonacci y la sección áurea, aunque denominándola incorrectamente como Theta (?) en vez de Phi (F).

El Número Áureo en la Música
Autores como Bártok, Messiaen y Stockhausen, entre otros, compusieron obras cuyas unidades formales se relacionan (a propósito) con la sección áurea. El compositor mexicano Silvestre Revueltas (1899-1945) utilizó también el número áureo en su obra Alcancías, para organizar las partes (unidades formales).
El grupo de rock progresivo norteamericano Tool, en su disco Lateralus (2001) hacen múltiples referencias al número áureo y a la secuencia Fibonacci, sobre todo en la canción que da nombre al disco, pues los versos de la misma están cantados de forma que el número de sílabas pronunciadas en cada uno van componiendo dicha secuencia. Además la voz entra en el minuto 1:37, que pasado al sistema decimal coincide muy aproximadamente con el número áureo.
La sección áurea en
el pentáculo
(Pentagrama, estrella
de cinco puntas) e xiste la relación del número
Vinci lo uso para
asentar en él al hombre de Vitruvio.
Gráficamente el número áureo es la relación entre el lado del pentágono regular y la recta que une dos vértices no consecutivos de éste. Si se toma como unidad un lado del pentágono interior, cualquier línea que marca los brazos de la estrella mide F. También la longitud total de cualquiera de las cinco líneas que atraviesan la estrella mide F3, mientras que la suma del lado interior y cualquiera de sus brazos es F2. Teniendo en cuenta la gran simetría de este símbolo se observa que dentro del pentágono interior es posible dibujar una nueva estrella, con una recursividad hasta el infinito. Del mismo modo, es posible dibujar un pentágono por el exterior, que sería a su vez el pentágono interior de una estrella más grande.
Gráficamente el número áureo es la relación entre el lado del pentágono regular y la recta que une dos vértices no consecutivos de éste. Si se toma como unidad un lado del pentágono interior, cualquier línea que marca los brazos de la estrella mide F. También la longitud total de cualquiera de las cinco líneas que atraviesan la estrella mide F3, mientras que la suma del lado interior y cualquiera de sus brazos es F2. Teniendo en cuenta la gran simetría de este símbolo se observa que dentro del pentágono interior es posible dibujar una nueva estrella, con una recursividad hasta el infinito. Del mismo modo, es posible dibujar un pentágono por el exterior, que sería a su vez el pentágono interior de una estrella más grande.
Al medir la longitud total de una de las cinco líneas del pentáculo interior, resulta igual a la longitud de cualquiera de los brazos de la estrella mayor, o sea F.
Qué es y de dónde
proviene el número áureo
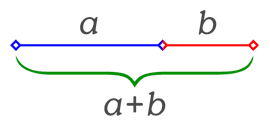
Se divide un segmento cualquiera en dos partes de forma que la razón entre
la totalidad del segmento y una parte (la mayor) sea igual a la razón entre
esta parte y la otra. Matemáticamente, siendo las partes a y b:
Esta razón, que cumple la propiedad, es denominada razón áurea. Se puede obtener este número a partir de la expresión anterior:
esión anterior:

Se puede despejar a utilizando la fórmula general de las ecuaciones de segundo grado, teniendo en cuenta que a > 0 y b > 0, o en otras palabras, tomando su valor positivo:

Dividiendo todo por b se obtiene:

Esta proporción del número de oro se presenta en todo el universo. Hoy día se presenta esta proporción áurea en objetos modernos como la tarjeta de crédito o débito, en los teléfonos celulares, televisores, símbolos o logos de compañía, instrumentos musicales, construcciones de edificios modernos y muchas cosas más. Tienes una tarea en tu vida, de descubrir lo bello que Dios ha creado en la naturaleza utilizando el número de oro, conocido como la proporción divina. Fibonacci presentó la sucesión en su libroLiber Abaci , publicado en 1202. Muchas propiedades de la sucesión de Fibonacci fueron descubiertas por Edouard Lucas, responsable de haberla denominado como se la conoce en la actualidad. Para más información puedes leer libros, revistas, buscar en la internet…
Ahora que estás familiarizado con la sucesión de
Fibonacci y el número de oro, puedes
contestar las siguientes dos preguntas:
11) ¿Quién fué Leonardo de Pisa (Fibonacci) y
Alberto Durero?
22) Menciona 3 elementos de la naturaleza relacionados con la
sección áurea.
3) ¿Como se relacionan el número de oro (sección áurea) y la sucesión de Fibonacci?
3) ¿Como se relacionan el número de oro (sección áurea) y la sucesión de Fibonacci?
Esta parte es opcional, pero puedes aprender más acerca de la Espiral de Durero.
Para que te diviertas: en un papel cuadriculado, construye la Espiral de Durero. Como se muestra aquí, lee las instrucciones para lograrlo.
Para que te diviertas: en un papel cuadriculado, construye la Espiral de Durero. Como se muestra aquí, lee las instrucciones para lograrlo.
3) De igual manera, trazará los
siguientes cuadrados que quepan en la hoja de la cuadricula. Formarás el
rectángulo áureo como se muestra abajo.
4)
Seguirás realizando el procedimiento hasta completar un rectángulo áureo que tiene las
proporciones del número de oro. Deberá visualizarse de esta manera vertical o
de manera horizontal si se cambia la perpectiva.
|
| ||||








No hay comentarios.:
Publicar un comentario